Punto medio de un segmento
PUNTO MEDIO DE UN SEGMENTO
Hallar el punto medio de un segmento, es uno de los cálculos o problemas básicos que abordarás más veces en tu desempeño académico relativo al campo de la geometría analítica. Tal vez, este requerimiento está tan frecuentemente solicitado como la distancia entre dos puntos, tema que ya hemos trabajado en un post anterior.
La cuestión es relativamente fácil cuando el segmento en cuestión, es paralelo a alguno de los dos ejes de coordenadas cartesianas, o mejor aún si está sobre uno de ellos. Piénsalo de esta manera: imagina un segmento horizontal que está posicionado sobre el eje de las “x” y que va desde el punto (3,0) hasta el punto (5,0). Rápidamente te das cuenta que el punto medio de ese segmento, está ubicado en el punto (4,0). Si lo piensas, más allá del evidente punto medio gráfico que deduces con sólo mirar la figura, esa coordenada 4, puede salir de sumar las dos coordenadas X del punto inicio y el punto final del segmento, y dividiendo entre dos. En otras palabras, sería (3+5) / 2 =8/2= 4.
Un razonamiento similar, surge del caso de imaginar el punto medio de un segmento paralelo al eje de las “y” o incluso un segmento definido sobre el mismo eje.
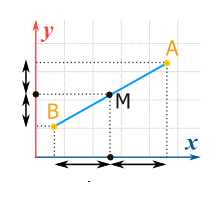
Ahora bien… ¿qué pasa cuando hablamos de un segmento oblicuo, tal como nos muestra la figura de portada? Te invito a seguir leyendo para aprenderlo todo acerca de cómo hallar el…
Punto medio de un segmento
Observa atentamente la imagen, en la que están marcados los puntos medios de las respectivas proyecciones a los ejes vertical y horizontal. El asunto es que el problema en esencia se remite al mismo concepto, y hallar el punto medio de este segmento que está en posición oblicua, consistirá ni más ni menos, en hallar los puntos medios de sus respectivas coordenadas “x” e “y”.
De hecho, en la siguiente imagen, podemos apreciar la fórmula por la que rápidamente puedes hallar el punto medio de un segmento de recta, siempre que conozcas las coordenadas de los extremos del mismo.
 Es muy importante puntualizar que cuando estás hallando el punto medio de un segmento, no estás buscando ninguna medida, sino las coordenadas de ese punto medio. Si miras la imagen con atención verás que la fórmula llama M al punto medio de cierto segmento, y que la coordenada “x” de ese punto M, se calcula sumando las x de los extremos y dividiendo entre 2, y lo mismo sucede con la coordenada “y”.
Es muy importante puntualizar que cuando estás hallando el punto medio de un segmento, no estás buscando ninguna medida, sino las coordenadas de ese punto medio. Si miras la imagen con atención verás que la fórmula llama M al punto medio de cierto segmento, y que la coordenada “x” de ese punto M, se calcula sumando las x de los extremos y dividiendo entre 2, y lo mismo sucede con la coordenada “y”.
Veamos un ejemplo y para razonarlo te invito a dibujar el mismo en una hoja de papel cuadriculada, representando el mismo en un par de ejes coordinados cartesianos:
Supongamos que queremos hallar las coordenadas del punto medio del segmento cuyos extremos son los puntos A (3,9) y B(-1,5).
Aplicando la fórmula antes señalada, sustituyendo las respectivas coordenadas x e y y operando, llegarás a calcular que las coordenadas del punto medio finalmente serán:
M( 1,7)
Créeme que utilizarás muchas veces este concepto, en especial cuando los datos de un problema te hablen de las diagonales de algunas figuras y uno de los retos sea calcular por donde se cruzan.
EN ESTE ESPACIO ENCONTRAREMOS EJERCICIOS DESARROLLADOS DE COMO ENCONTRAR EL PUNTO MEDIO DE UN SEGMENTO.
VÍDEOS COMPLEMENTARIOS PARA ESTUDIAR:
Comentarios
Publicar un comentario